Click here👆to get an answer to your question ️ A solution of the equation (1 tan x )(1 tan x) sec^2x 2^tan^2 = 0 , where x lies in the interval pi2, pi2 is given by$$\int sec^2x \tan^2x dx = tan^2x 2\int \sec^2x \tan^2x dx$$ You can move the $ 2\int \sec^2x \tan^2x dx$ to the left hand side of the equation by addition $$\int \sec^2x \tan^2x dx 2\int \sec^2x \tan^2x dx= tan^2x c, c\in\mathbb{R}$$ Note that once we have a side without an integral on it you need to include a constant of integrationRewrite sec(x) sec ( x) in terms of sines and cosines Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by 1 cos(x) 1 cos ( x) Write cos(x) cos ( x) as a fraction with denominator 1 1 Cancel the common factor of cos(x) cos ( x)
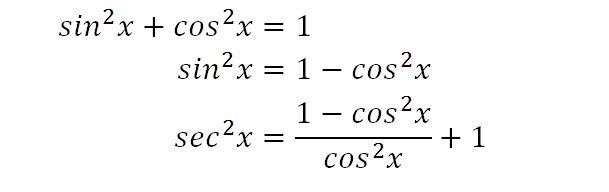
Integrate Sec 2x Method 2
Tan^2(x) + 1 = sec^2(x) proof
Tan^2(x) + 1 = sec^2(x) proof-About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators prove that cot x tan 2x1 =sec 2x Trigonometry Verify the identity algebraically TAN X COT Y/TAN X COT Y= TAN Y COT X Math Factorthen use fundamental identities to simplify the expression below and determine which of the following is not equivalent cot^2 a * tan^2 a cot^2 a A csc^ 2 alpha B1/ sin^ 2 alpha C1/ 1cos^ 2 alpha D




Get Answer 1 Tan2x Sec2x Dx Sin2x 2 C Tan 2 X 2 C 2sin X Cos X Transtutors
Unlock StepbyStep derivative of sec^2 (x) Extended Keyboard Examples heart 22 profile rohinishiva17 Answer LHS= (sec^2)^3 (tan^2)^3 = (sec^2tan^2)^33sec^2*tan^2 (sec^2tan^2) = (1)^33 (1tan^2x)tan^2x (1) (sec^2xtan^2x)=1In this video you will learn how to verify trigonometric identitiesverifying trigonometric identitieshow to verify trig identitieshow to verify trigonometric
Rewrite 12 sec2(x) 1 2 sec 2 ( x) as ( 1 sec(x))2 ( 1 sec ( x)) 2 Rewrite sec(x) sec ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by 1 cos(x) 1 cos ( x) Multiply cos(x) cos ( x) by 1 1Differentiate c and d, use the product rule to find v Then just use the product rule on u and v 0See the answer tan^2x−1/sec^2x=tan x−cotx/tan xcot x solution and steps please Expert Answer 100% (1 rating) Previous question Next question
Question 2502 prove that tanx (cotxtanx)=sec^2x i have no idea how to do this please help thank you Answer by Fombitz () ( Show Source ) You can put this solution on YOUR website!In Trigonemetry Laws and Identities, there are some rule that we will use to prove 1 / sec² (x) = cos² (x) * tan² (x) 1 = sec² (x) * sin² (x) cos² (x) = 1 * tan (x) = sin (x) / cos (x) We will prove from the Left Hand Side We know that sec²{eq}\frac{(\tan 2x)}{(1 \sec 2x)} = \tan x {/eq} Identities in Trigonometry The identities are trigonometric equations, in that, any value of the variable contained by the equation can make the




How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Homeworklib




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
True or false the equation tan^2x1=sec^2x Get the answers you need, now!We get (tan(x))2 1 = (sec(x))2 1 = (sec(x))2 (tan(x))2 Now, we will see if 1 = (sec(x))2 (tan(x))2and 1 = (sec(x))2 (tan(x))2 canSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




How Many Can You Derive From First Principles Ppt Download




The Derivative Of Tan 2x Derivativeit
Keep breaking it down until you find something you can work with Let u=sec^2 and v=tan^2 and if that's still too much at this stage Let a=sec b=sec c=tan d=tan Differentiate a and b, use the product rule to find u; A few hints 1 sec x = 1/(cos x) 2 (sin x)/(cos x) = tan x That should give you a good start$\begingroup$ so mu next step would be $2\ln((\tan x)) \cdot ln(tan)^2x\ cdot\frac{1}{sec^2x}$ $\endgroup$ – Sunny Jul 4 '15 at 07 Add a comment 5 Answers Active Oldest Votes 1 $\begingroup$ You make mistakes when applying the chain rule The function you are differentiating is




Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction




Ashley Avery Free Books Catalog
Verify (1tan^2x)/(1cot^2x) = 1sec^2x Answered by a verified Math Tutor or Teacher We use cookies to give you the best possible experience on our website By continuing to use this site you consent to the use of cookies on your device as described in our cookie policy unless you have disabled them$$ \tan^2x \sec^2x $$ $$ (\sin x / \cos x)^2 (x / \cos x)^2 $$ trigonometry Share Cite Follow edited Jan 17 '13 at 644 Paul 177k 3 3 gold badges 49 49 silver badges 77 77 bronze badges asked Jan 17 '13 at 639 sam sam 61 1 1 gold badge 3 3 silver badges 6 6 bronze badges $\endgroup$ 1 4Calculus 2, integral of (1tan^2x)/sec^2x, integral of cos(2x)



True Or False The Equation Sec 2 X 1 Tan 2 X Is An Identity Brainly Com




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
Hi Simplifying the following (sec^2x csc^2x) (tan^2x cot^2x) tan^2x = sec^2x 1 cot^2x = csc^2x 1 (sec^2x csc^2x) (sec^2x 1 csc^2x 1)= 2We know, $$\csc^2x\cot^2x=1=\sec^2x\tan^2x$$ Share Cite Follow answered Sep 30 '13 at 1430 lab bhattacharjee lab bhattacharjee 266k 17 17 gold badges 192 192 silver badges 304 304 bronze badges $\endgroup$ Add a comment 2 $\begingroup$Free trigonometric identities list trigonometric identities by request stepbystep




Which Of The Following Expressions Completes The Identity 1 Sec 2 X Mathematics Stack Exchange



1
\(1\tan^2x = \sec^2x\) (the Pythagorean Theorem) If the integrand can be manipulated to separate a \(\sec^2x\) term with the remaining secant power even, or if a \(\sec x\tan x\) term can be separated with the remaining \(\tan x\) power even, the Pythagorean Theorem can be employed, leading to a simple substitutionAdal2762 adal2762 Mathematics Middle School answered True or false the equation tan^2x1=sec^2x 1 See answer adal2762 is waiting for your help Add your answer and earn points kudzordzifrancis kudzordzifrancisSec^2xtan^2x= 1 1cot^2x= csc^2x cot^2x= csc^2x1 csc^2xcot^2x= 1 YOU MIGHT ALSO LIKE 8 Basic Trig Identities 8 terms kovoquiz Algebra trig identities 11 terms clairebelfore Trigonomentry Formula 13 terms harini_chandrasekar Sin, Cos, Tan Equations 12 terms michellebarth OTHER SETS BY THIS CREATOR




Answered 3 1 Tanx Tan 2x Sec 2x S Bartleby



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero
Click here👆to get an answer to your question ️ If sec x sec^ 2x = 1 then the value of tan^ 8 tan^ 4 2tan^ 2x 1 will be equal to Trig Use the fundamental identities to simplify the expression cot beta sec beta I used 1tan^2u=secu since cot is the inverse of tan I flipped the tangent, then so it was 1 (1/tan)Math\int \frac{1\tan^2x}{1\tan^2x} \,dx/math math\int \frac{1\tan^2x}{\sec^2x} \,dx/math math\int \frac{1\tan^2x}{\frac{1}{\cos^2x}} \,dx/math math
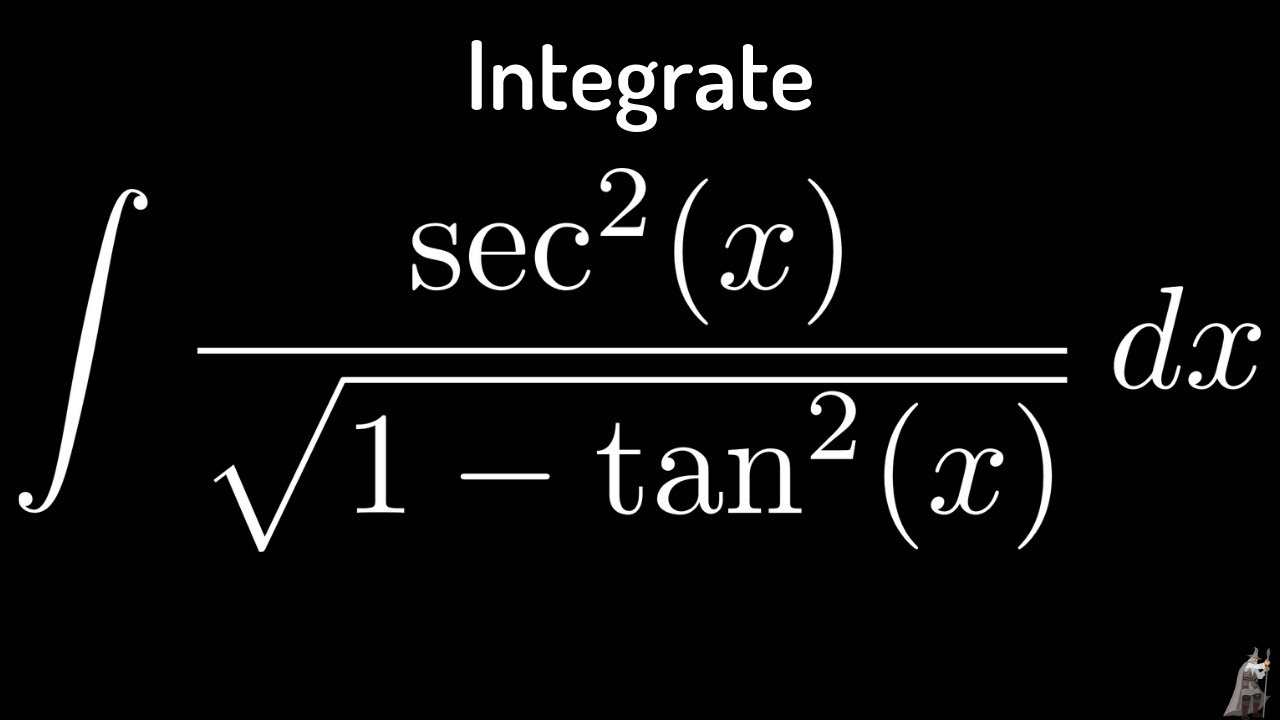



Integral Of Sec 2 X Sqrt 1 Tan 2 X Using The Arcsine Function Youtube




Tan 2x 2tanx 5dy Dx 2 1 Tanx Sec 2x Differential Equations Brainly In
Terms in this set (8) sin^2xcos^2x =1 tan^2x1 sec^2x 1cot^2x =csc^2xThe derivative of ax^ {n} is nax^ {n1} The derivative of a polynomial is the sum of the derivatives of its terms The derivative of a constant term is 0 The derivative of a x n is n a x n − 1 \sec (2x^ {1}1)\tan (2x^ {1}1)\times 2x^ {11} sec ( 2 x 1 − 1) tan ( 2 x 1 − 1) × 2 x 1 − 1 Simplify(sec x 1)(sec x 1) = tan^2 x




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




Which Equations Below Represent Pythagorean Proper Gauthmath
Answer to Solve the trigonometric equation on the interval \\parenthesis 0,2\\pi \\parenthesis \\tan(2x) 1 = \\sec(2x) By signing up, you'll get When trying to prove trig identities, it is often helpful to convert TAN functions into SIN/COS functions Proof Step 1 Start with the original equation to prove tan 2 x sin 2 x = (tan 2 x)(sin 2 x) Proof Step 2 Replace tan with sin/cos (sin 2 x/cos 2 x) sin 2 x = (sin 2 x/cos 2 x)(sin 2 x) Proof Step 3 Obtain a common denominator on left, simplify right (sin 2 x sin 2 x cos 2 x`1 tan^2x = 1tan^ 2 x` ANSWER The last line proves the identity`tan x(cot x tan x) = sec^2 x` Approved by eNotes Editorial Team Tushar Chandra Educator since 10 12,615 answers




Sec 8x 1 Sec 4x 1 Tan 8x Tan 2x Maths Trigonometric Functions Meritnation Com




Int Tanx Sec 2x Sqrt 1 Tan 2x Dx
Learn how to solve simplify trigonometric expressions problems step by step online Simplify the trigonometric expression 1/(sec(2x)tan(2x))(2sec(2x)*tan(2x)2sec(2x)^2) Multiply the fraction and term Factor the polynomial 2\sec\left(2x\right)\tan\left(2x\right)2\sec\left(2x\right)^2 by it's GCF 2\sec\left(2x\right) Ex 34, 8 Find the general solution of the equation sec2 2x = 1 – tan 2x sec2 2x = 1 – tan 2x 1 tan2 2x = 1 – tan2x tan2 2x tan2x = 1 – 1 tan2 2x tan2x = 0 tan 2x (tan2x 1) = 0 Hence We know that sec2 x = 1 tan2 x So, sec2 2x = 1 tan2 2x tan 2x = 0 taSeparate fractions Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by sin(x) cos(x) sin ( x) cos ( x) Convert from cos(x) sin(x) cos ( x) sin ( x) to cot(x) cot ( x) Divide sec2(x) sec 2 ( x) by 1 1 Rewrite sec(x) sec ( x) in terms of sines and cosines




Integrate Sec 2x Method 1




Solution 3 Sec Maths Studypool
Solve for x tan (2x)=1 tan (2x) = 1 tan ( 2 x) = 1 Take the inverse tangent of both sides of the equation to extract x x from inside the tangent 2x = arctan(1) 2 x = arctan ( 1) The exact value of arctan(1) arctan ( 1) is π 4 π 4 2x = π 4 2 x = π 4 Divide each term by 2 Well, if we divide (cos(x))2 on both sides;2 x I started this by making sec 1/cos and using the double angle identity for that and it didn't work at all in any way ever Not sure why I can't do that, but something was wrong Anyways I looked at the solutions manual and they magic out 1 tan x tan 2 x = 1 tan




Consider The Following Equations 1 Cosec 2x Sec 2x Cosec 2xsec 2x 2 Sec 2x Tan 2x Sec 2xtan 2x 3 Cosec 2x Tan 2x Cot 2x




Tan 2 X Tan 2 X 1 Cosec 2 X Sec 2 X Cosec 2 X 1 Sin 2 X Cos 2 X Brainly In
Question Tan^2x−1/sec^2x=tan X−cotx/tan Xcot X Solution And Steps Please This problem has been solved!Verify the Identity cot (x)^2 (sec (x)^21)=1 cot2 (x) (sec2 (x) − 1) = 1 cot 2 ( x) ( sec 2 ( x) 1) = 1 Start on the left side cot2(x)(sec2(x)−1) cot 2 ( x) ( sec 2 ( x) 1) Apply pythagorean identity cot2(x)tan2(x) cot 2 ( x) tan 2 ( x) Convert to sines and cosines Tap for more steps Write cot ( x) cot ( x) in sines and cosines Left hand side is cosx1/tan^2x and the right hand side is cosx/secx1 Click to expand \ Lcos(x) 1 tan2(x) = cos(x) sec(x) − 1 \L cos Since this is not actually an identity, you only need to find an xvalue for which the two sides are unequal, and you're done!
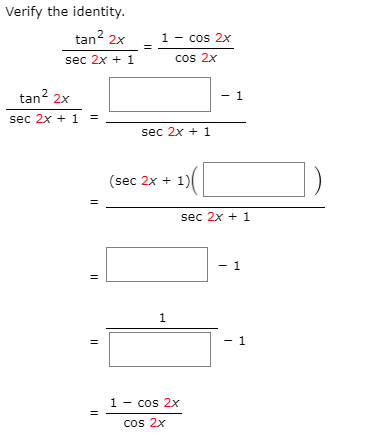



Verify The Identity Tan 2x 1 Cos 2x Cos 2x Sec 2x Chegg Com
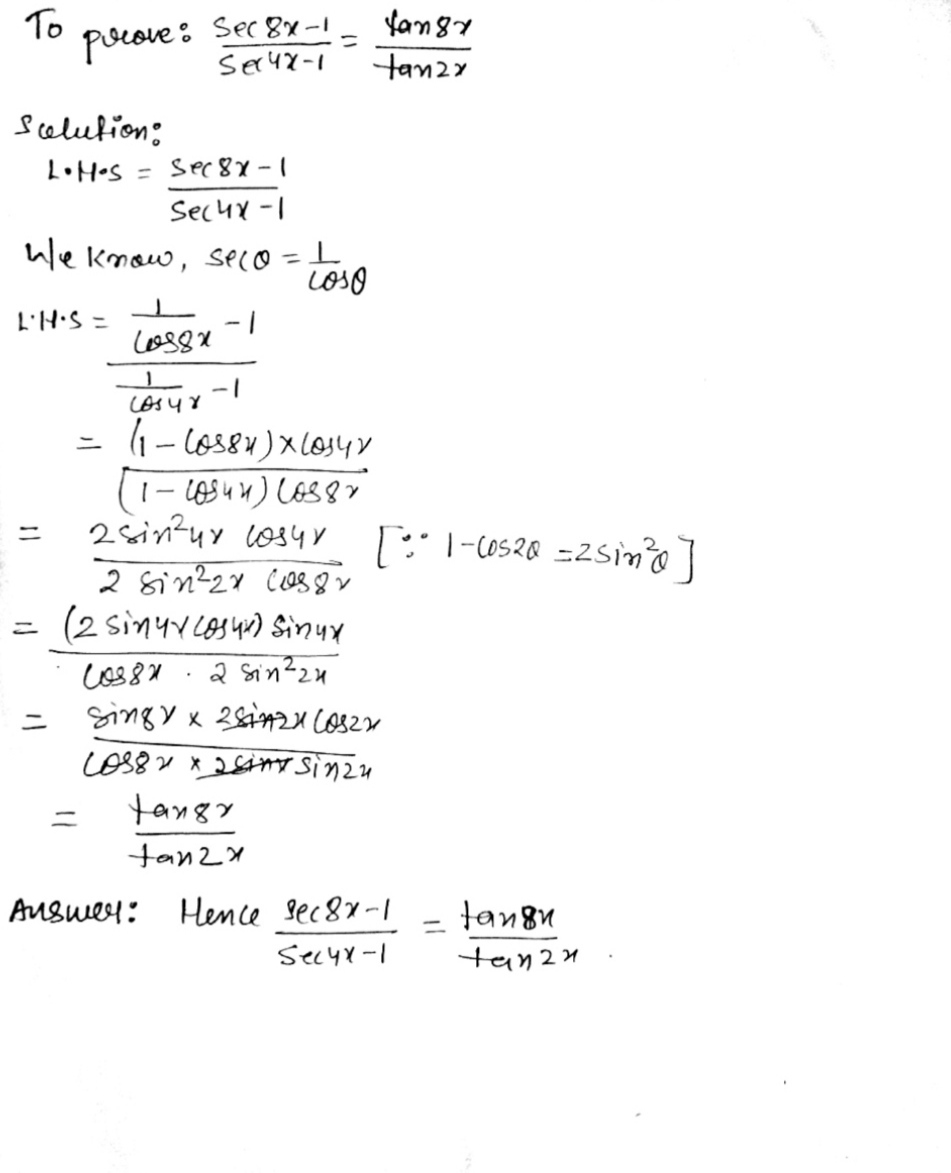



Prove That Frac Mathit Sec 8x 1 Mathit Sec 4x 1 Frac Tan 8x Tan 2x Snapsolve
Note that `tan^2x1=sec^2x=1/(cos^2x) ` and `tan^2x=(sin^2x)/(cos^2x) ` Substituting we get `(tan^2x)/(1tan^2x)=((sin^2x)/(cos^2x))/(1/(cos^2x))=sin^2x ` as required Explanation Start with the well known pythagorean identity sin2x cos2x ≡ 1 This is readily derived directly from the definition of the basic trigonometric functions sin and cos and Pythagoras's Theorem Divide both side by cos2x and we get sin2x cos2x cos2x cos2x ≡ 1 cos2x ∴ tan2x 1 ≡ sec2xCot (x) = cot (x) sin ^2 (x) cos ^2 (x) = 1 tan ^2 (x) 1 = sec ^2 (x) cot ^2 (x) 1 = csc ^2 (x) sin (x y) = sin x cos y cos x sin y cos (x y) = cos x cosy sin x sin y tan (x y) = (tan x tan y) / (1 tan x tan y) sin (2x) = 2 sin x cos x cos (2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x)



1




Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified
Found 2 solutions by ewatrrr, MathLover1 Answer by ewatrrr () ( Show Source ) You can put this solution on YOUR website! See the proof below We need tanx=sinx/cosx sin^2xcos^2x=1 secx=1/cosx Therefore, LHS=tan^2x1 =sin^2x/cos^2x1 =(sin^2xcos^2x)/cos^2x =1/cos^2x =sec^2x =RHS QED Trigonometry Science




Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube
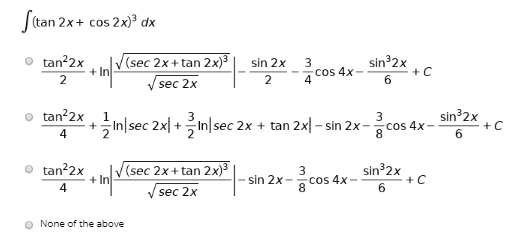



Answered Stan 2x Cos 2x Dx Tan 2x 2 V Sec 2x Bartleby




Trig Identity Sec2x Minus Tan2x T10 Youtube




How To Prove That Math Frac Sec 8x 1 Sec 4x 1 Frac Tan 8x Tan 2x Math Quora




1 1 Csc Or Sin Or Csc Sin 1 Sin Csc X X X X X X 1 1 Sec Or Cos Or




Answered Find The Indefinite Integral Sec 2x Bartleby




Evaluate Int Tanxsec 2x 1 Tan 2x Dx
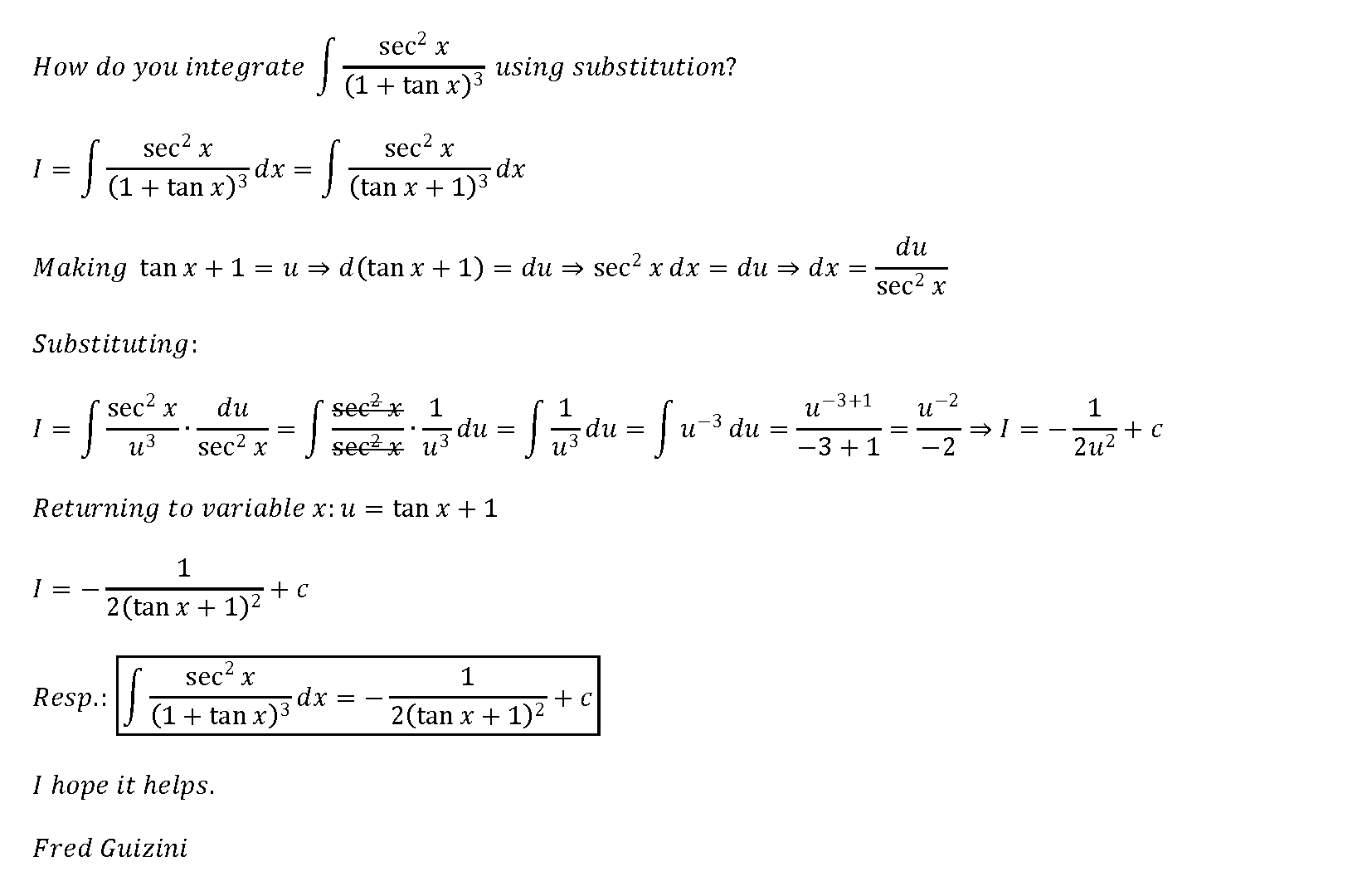



How Do You Integrate Int Sec 2x 1 Tanx 3 Using Substitution Socratic
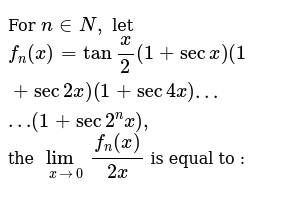



For N In N Let F N X Tan X 2 1 Sec X 1 Se




2 Prove The Following Trig Identities A Prove Tan Chegg Com




3 Sec 2x1 Cos 2x Tan 2x Tan X Esus Is Always The Anse Ja Irl Meme On Me Me
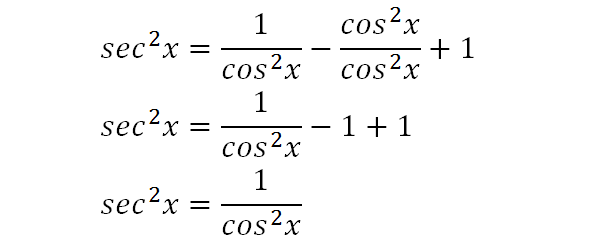



Integrate Sec 2x Method 2



What Is The Differentiation Of Sec Inverse Tan 2x Quora
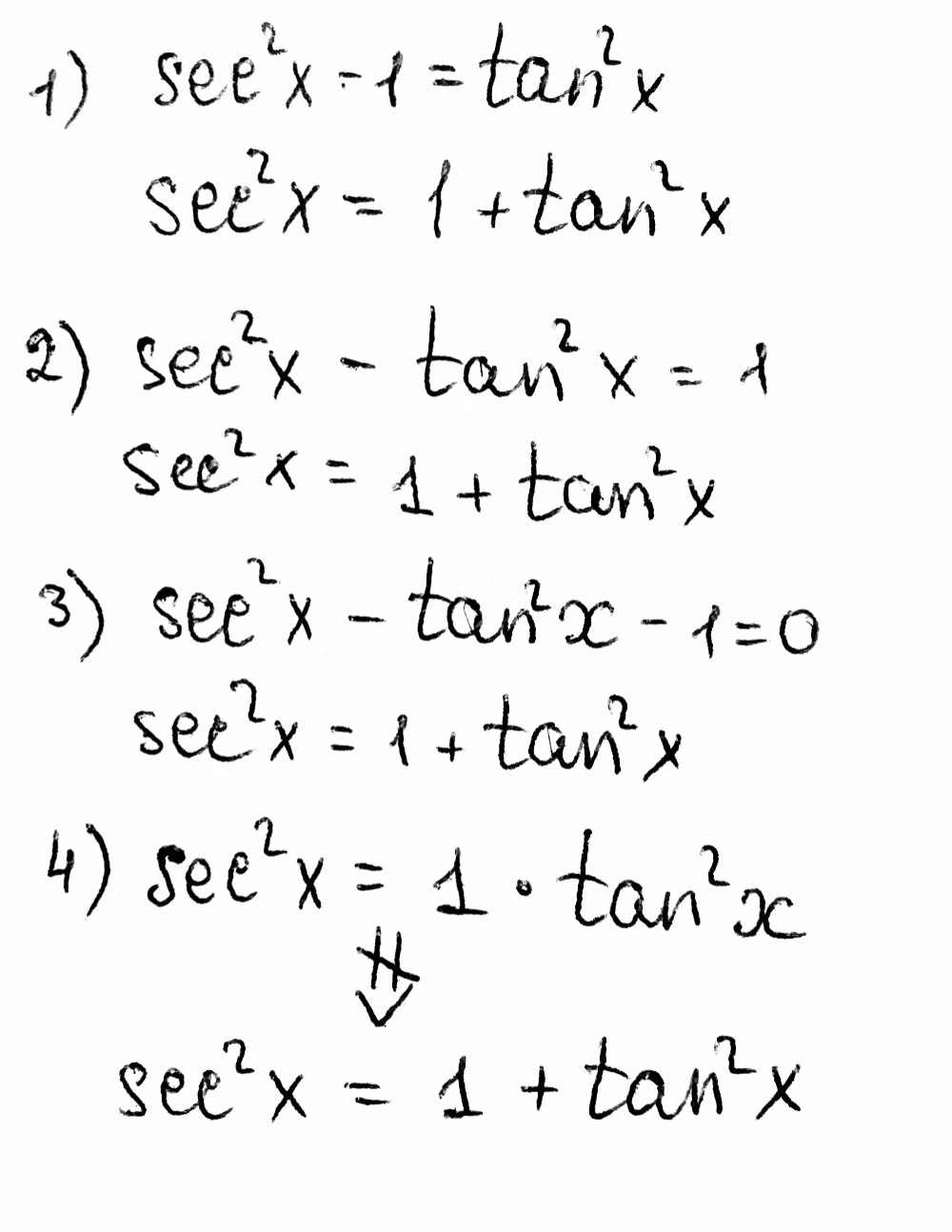



Which One Is Not Equivalent To Sec2x 1 Tan2x Sec Gauthmath




F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2
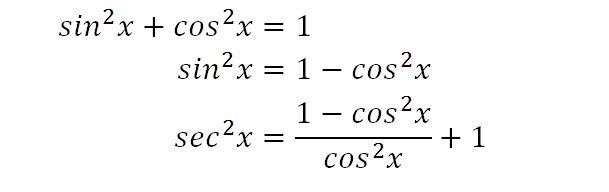



Integrate Sec 2x Method 2
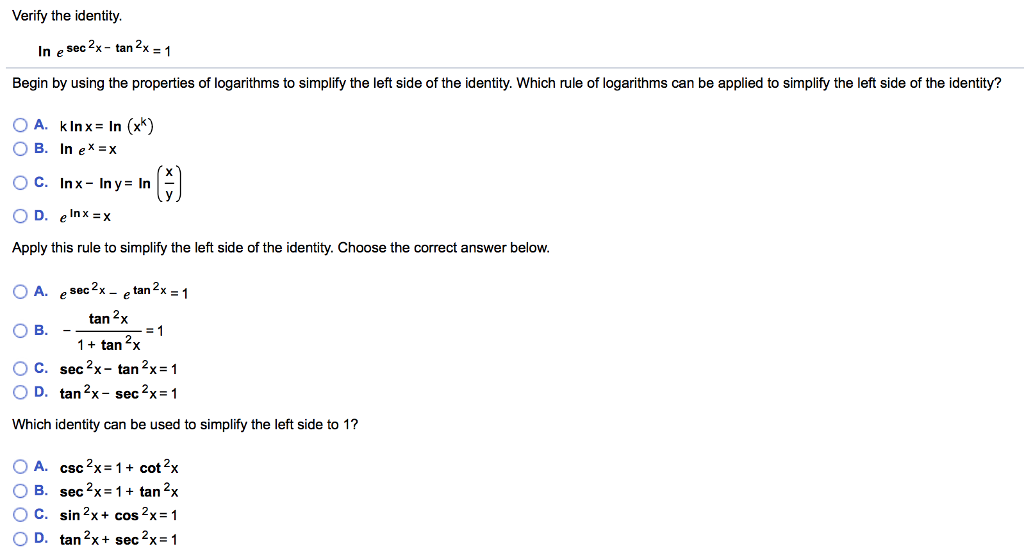



Verify The Identity In Esec 2x Tan 2x 1 Begin By Chegg Com




Proof Tan 2 1 Sec 2 Youtube




Analytic Trig Ppt Video Online Download




3 Sin Differentiate The Following Functions With Respect Tox 1 Sin 2x 4 Sin 1 Ax




3 Sec 2x1 Cos2 X Tan 2x Tantx E Sus S Always The An 0 Om Reddit Meme On Me Me




Get Answer 1 Tan2x Sec2x Dx Sin2x 2 C Tan 2 X 2 C 2sin X Cos X Transtutors




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube




2 Prove The Following Trig Identities A Prove Tan Chegg Com
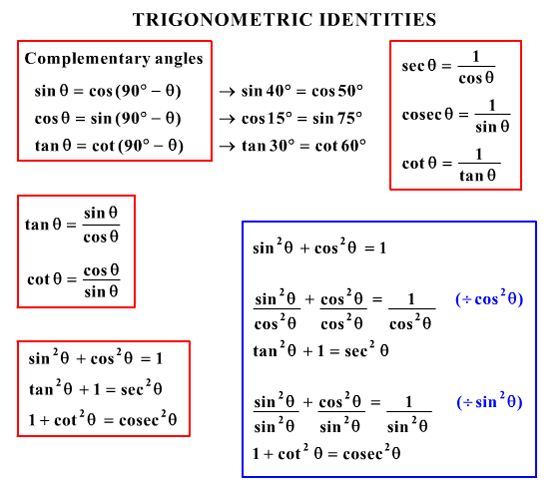



What Would Be Steps In Proving That Tan2x Secx 1 1 Sec X Socratic
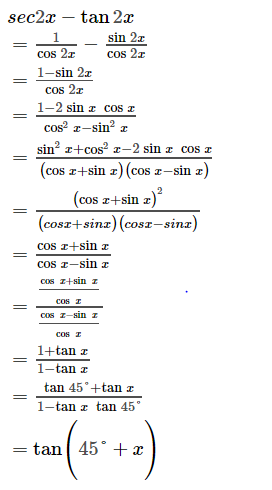



Sec2x Tan2x If0 X P 4




Solution Calculations Studypool



2



Math Problems Simplifying With Trigonometry Identities And Then Integration
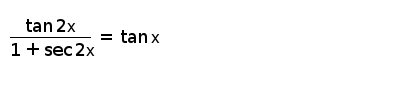



Tan 2x 1 Sec 2x Tan X



Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero
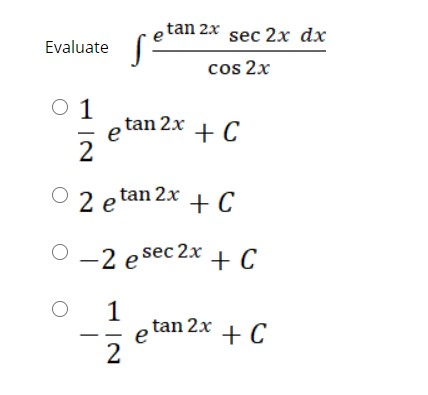



Answered Tan 2x Sec 2x Dx Evaluate Cos 2x O 1 Bartleby




Integral 1 Tan 2 X Sec 2 X Youtube




2 Prove The Following Trig Identities A Prove Tan Chegg Com




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic




Ch Ppt Download




Limit Trigonometric Function 2 Sec 2x 1 Tan X Youtube




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic



Tan2x ただの悪魔の画像




Sec 6x Tan 6x 1 3 Tan 2x Sec 2x Brainly In




Find The General Solution For Each Of The Following Equations Sec2 2x 1 Tan 2x Mathematics Shaalaa Com




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



Chapter 5



Differentiate The Sec 1 1 Tan 2x 1 Tan 2x W R T X Sarthaks Econnect Largest Online Education Community
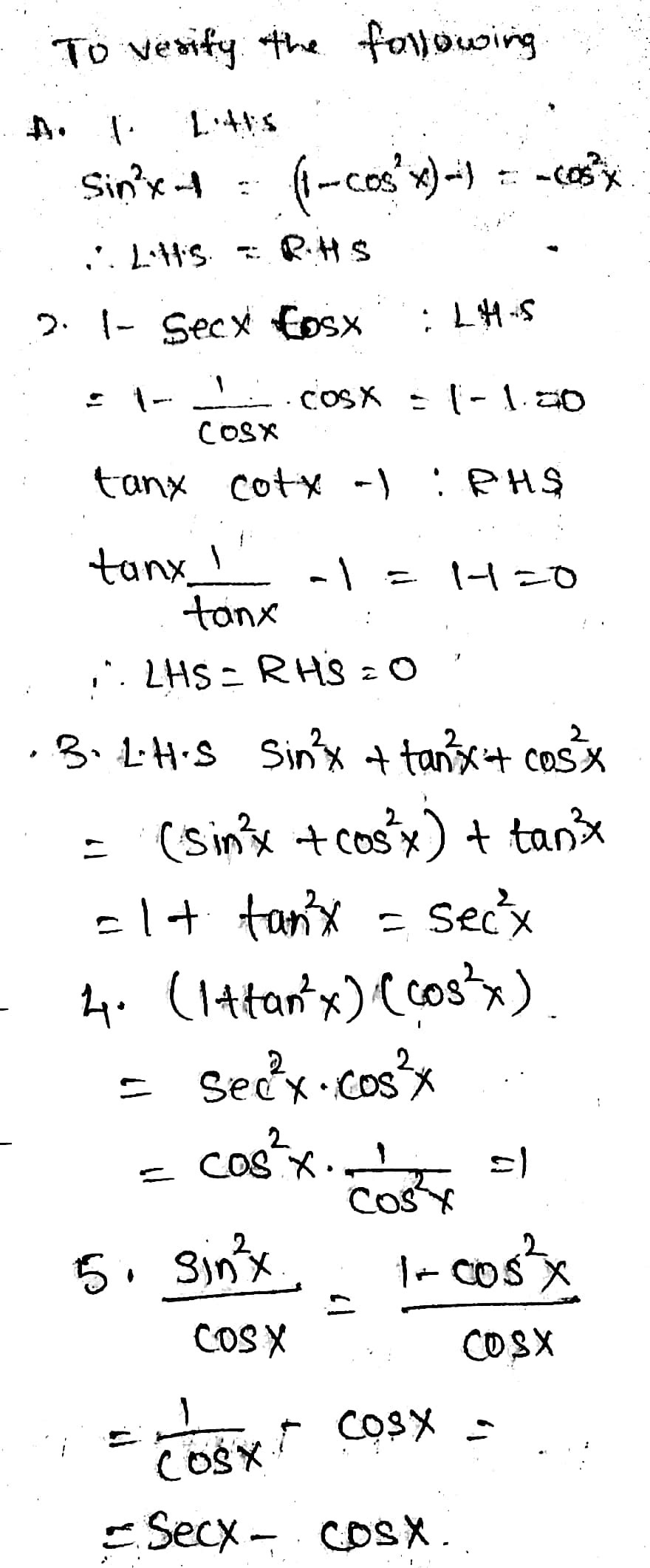



Directions Verify The Following Trigonometric Id Gauthmath




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
x-1=sec(squared)x.jpg)



10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com




8 Solve The Equation Sec C22x See How To Solve It At Qanda




How To Show That Math Tan 2 X Sec 2 X 1 Math Quora




Tan 2x 1 Sec 2x Tan X Sin X Cos X 2 1 Sin 2x Youtube
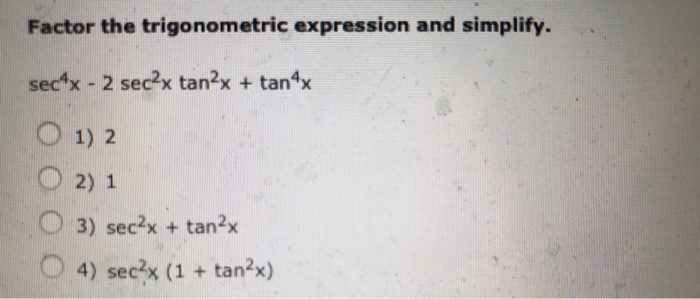



Factor The Trigonometric Expression And Simplify Chegg Com



Tan 2x Sec 2x 1 Sec 2x Tan 2x 1 10 12 2 Sarthaks Econnect Largest Online Education Community



View Question Please Help
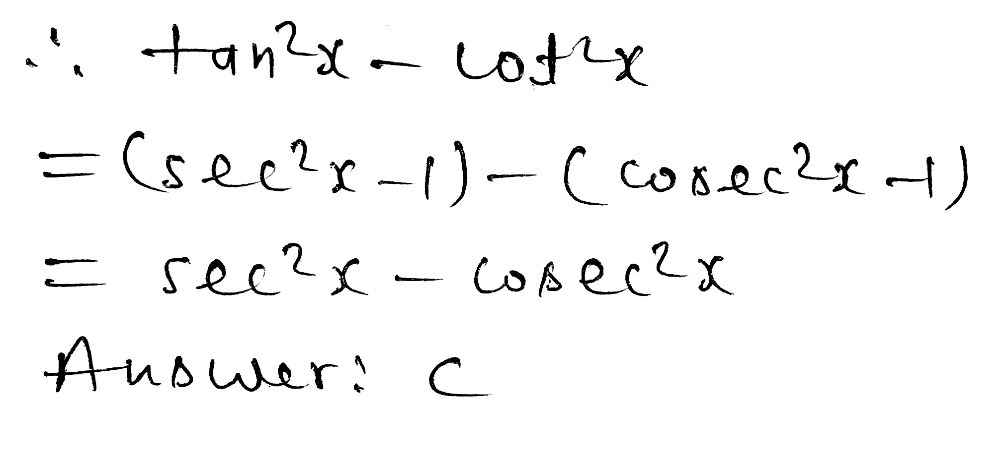



Use Trig Identities To Simplify Tan 2x Cot 2x A Gauthmath




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic




Mathematics Question Of The Day With Solution Facebook



1




Trigonometric Identity In Double Angle Sin2x Cos2x 1 Sin2x Cos2x 1 Sec2x Tan2x Youtube




Solved 12 Evaluate The Integral Tan 2x 1 Sec 2x 1 Chegg Com




4 Tan 2x 2 Sec 2x 1 0 X In 0




How Do You Integrate 1 Tan2x Sec2x Dx Socratic



View Question For Questions 1 5 Decide Whether The Equation Is A Trigonometric Identity Explain Your Reasoning
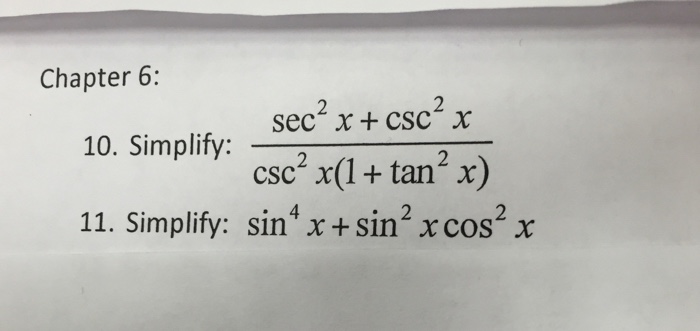



10 Simplify Sec 2x Csc 2x Csc 2x 1 Tan 2x 11 Chegg Com



2




Verify The Identity 4 2 Tan X Secx2tan X 1 Which Chegg Com



1




Iit 1994 Prove That Sec2x Tan2x Tan Pi 4 X When X Lies Between 0 And Pi 4 Youtube
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




Tan 2x 1 Sec 2x Tan X




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic




Integrate Sec 2x Method 2
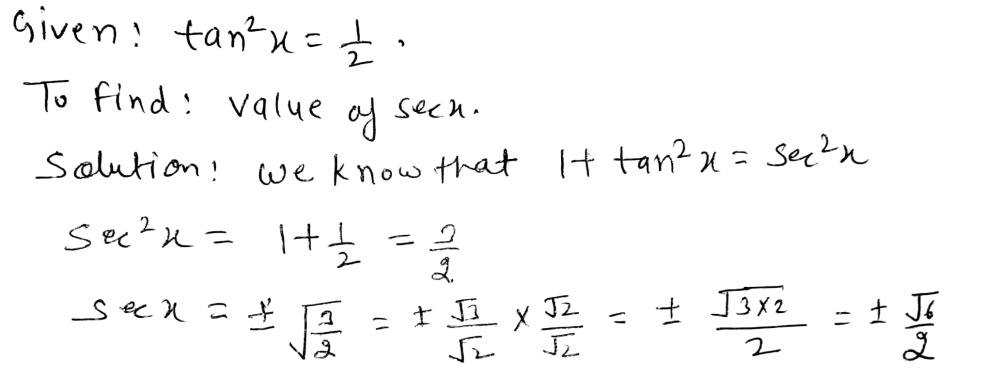



46 Find Sec X If Tan 2x 1 2 A 1 4 B Gauthmath



Prove That Sec 4x Sec 2x Tan 2 X Tan 4x




3 Sec 2x1 Cos 2 X Tan 2 X Tantx Esus Is Always The An 小 Ts Sec Meme On Me Me




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic




How To Show That Math Tan 2 X Sec 2 X 1 Math Quora



No comments:
Post a Comment